Tal como indica el título, vamos a construir con TensorFlow una red siamesa que aceptará dos entradas y nos dirá el grado de similitud entre las dos imágenes, para que podamos decidir si se tratan o no del mismo tipo.
Se puede encontrar el código fuente y copiarlo o crear un duplicado en Kaggle:
https://www.kaggle.com/code/peremartramanonellas/how-to-create-a-siamese-network-to-compare-images
Para el ejemplo he usado el famoso dataset MNIST, que está formado por más de 4000 imágenes de números escritos a mano de 28×28. Trataremos de entrenar un modelo que sea capaz de reconocer si los dos números pasados al sistema son él mismo o no.
If you are looking for the English version of this article, it is here:
Breve explicación de cómo funciona una red siamesa.
Las redes siamesas disponen de dos entradas y las compara para indicarnos cuánto de iguales o diferentes son. Nos permite decidir si las imágenes son de un mismo tipo. En nuestro caso nos permitirá decidir si se trata del mismo número o no.
De cada una de las entradas calcula un vector, y entonces usa ese vector para calcular la Distancia Euclidiana.
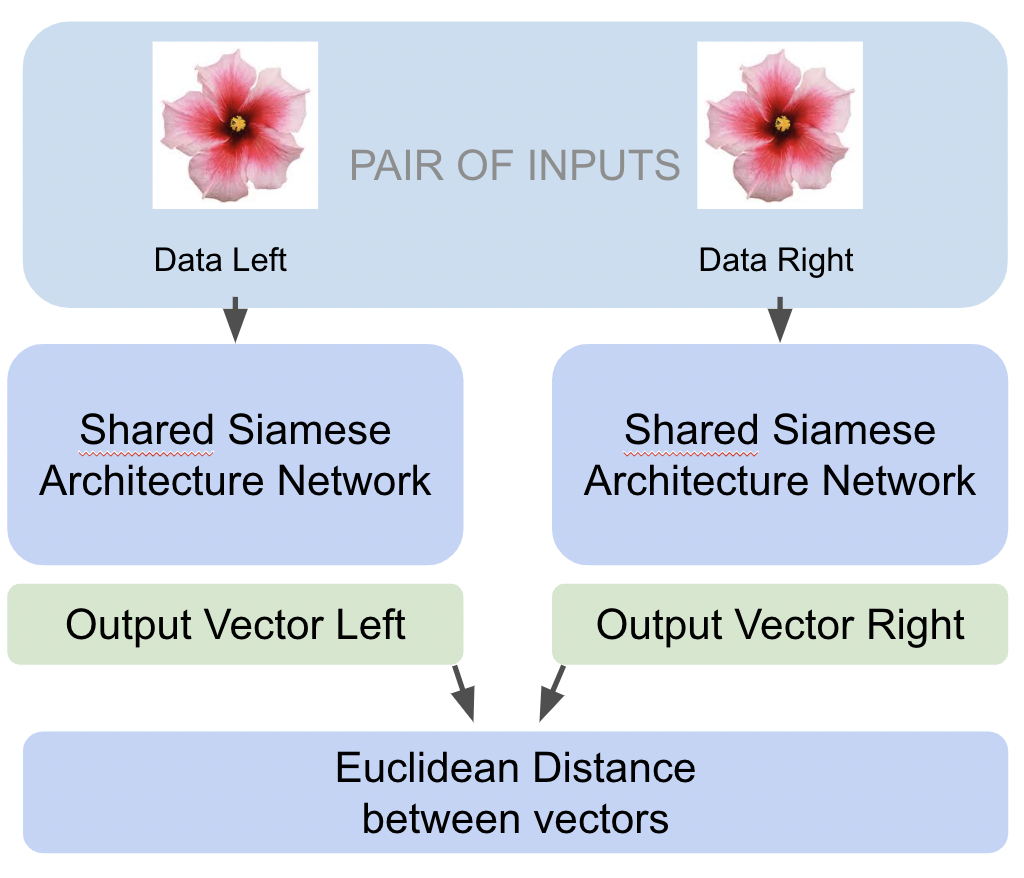
El sistema tan solo nos devuelve un número, somos nosotros los responsables de decidir cuando esta valoración de las diferencias nos esta indicando qué se trata, o no de la misma imagen. Cuanto menor sea el número devuelto, menos serán las diferencias. Para dos elementos idénticos el sistema devolverá un 0.
¿Cuándo puede usarse una red siamesa?
Aunque son muy usadas en reconocimiento facial, las redes Siamesas no se limitan al campo de las imágenes. Pueden ser usadas para detectar similitudes en muchos campos.
Por ejemplo, en NLP, se usan para identificar contenido duplicado, o para saber si dos noticias o tweets tratan de un mismo tema.
Pueden usarse también para reconocimiento de ficheros de Audio, por ejemplo, para comparar voces y saber si pertenecen a la misma persona.
Las redes siamesas funcionan siempre que queramos comparar dos Items entre ellos, sean del tipo que sean, y son especialmente aconsejadas cuando en Dataset de entreno es limitado. Ya que al poder emparejar de forma diferente los Items disponibles aumentamos la información que podemos obtener de los datos.
En el ejemplo he emparejado cada Item con otro de la lista, pero podría haber emparejado cada Item con el resto, lo que nos daría un juego de datos impresionantemente gigante. Esta posibilidad de combinación nos permite disponer de suficientes datos de entreno por muy pequeño que sea el Dataset.
Tratamiento de los datos.
Para ver el código completo lo mejor es que tengáis abierto el link al notebook en Kaggle. Aquí veremos tan solo una parte, la más especifica, a la creación de una red Siamesa.
Crear parejas de números:
#The third parameter: min_equals. indicate how many equal pairs, as minimun, we want in the dataset.
#If we just created random pairs the number of equal pairs would be very small.
def create_pairs(X, y, min_equals = 3000):
pairs = []
labels = []
equal_items = 0
#index with all the positions containing a same value
# Index[1] all the positions with values equals to 1
# Index[2] all the positions with values equals to 2
#.....
# Index[9] all the positions with values equals to 9
index = [np.where(y == i)[0] for i in range(10)]
for n_item in range(len(X)):
if equal_items < min_equals:
#Select the number to pair from index containing equal values.
num_rnd = np.random.randint(len(index[y[n_item]]))
num_item_pair = index[y[n_item]][num_rnd]
equal_items += 1
else:
#Select any number in the list
num_item_pair = np.random.randint(len(X))
#I'm not checking that numbers is different.
#That's why I calculate the label depending if values are equal.
labels += [int(y[n_item] == y[num_item_pair])]
pairs += [[X[n_item], X[num_item_pair]]]
return np.array(pairs), np.array(labels).astype('float32')
Esta función se recorre cada uno de los elementos en el Dataset y los empareja con otro elemento, dando como resultado un número de parejas iguales al de elementos del dataset. Para asegurarnos de que hay un número mínimo de elementos con parejas del mismo tipo se ha incorporado el parámetro min_equals. Las primeras parejas, hasta llegar a min_equals, se crearán con elementos del mismo tipo, el resto se emparejan de forma aleatoria.
En las últimas líneas se puede ver cómo se generan las parejas y se guardan en la variable pairs. Sus etiquetas se guardan en la variable labels.
Los datos se transforman en el return para que sean tratables desde el modelo.
A destacar esta línea al principio de la función: index = [np.where(y == i)[0] for i in range(10)]. Nos produce un array llamado índice de 9 filas. Cada fila contiene las posiciones de los números, en el array de etiquetas (y) que pertenecen a la categoría indicada.
Es decir, para index[0] Tendremos todas las posiciones, en el array y de los números con valor 0. En Index[1] las posiciones del valor 1…
Creando el Modelo Siames
Antes de crear el modelo hay que hacer tres funciones. Una para calcular la distancia euclideana entre los dos vectores que acaba generando el modelo. Otra para modificar el shape de los datos de salida. La tercera es la función de loss que nos sirve para calcular la pérdida. No sufráis, es una función, diría que, standard para todos los modelos Siameses.
def euclidean_distance(vects):
x, y = vects
sum_square = K.sum(K.square(x - y), axis=1, keepdims=True)
return K.sqrt(K.maximum(sum_square, K.epsilon()))
def eucl_dist_output_shape(shapes):
shape1, shape2 = shapes
return (shape1[0], 1)
def contrastive_loss_with_margin(margin):
def contrastive_loss(y_true, y_pred):
square_pred = K.square(y_pred)
margin_square = K.square(K.maximum(margin - y_pred, 0))
return (y_true * square_pred + (1 - y_true) * margin_square)
return contrastive_loss
La función de Loss, contrastive_loss, esta anidada dentro de otra función, contrastive_loss_with_margin, para que nos permita pasarle un parámetro. Pero se podría haber obviado y usar siempre el mismo valor en margin.
Al crear el modelo la función de loss se le pasa al método compile, y este es el responsable de pasar los parámetros y_true e y_pred para que se pueda calcular la perdida en cada paso. Nosotros no podemos pasar mas parámetros, por eso anidamos la función. Realmente el método compile lo que recibe es la función de loss que espera los datos de entrada y_true e y_pred.
La función nos devolverá un valor positivo alto en caso de que los elementos sean diferentes, y lo irá reduciendo a medida que se encuentren más similitudes.
Ytrue * Ypred2 + (1 -Ytrue) * max(margin-Ypred, 0)2
La fórmula matemática adaptada a las variables es la que vemos arriba. Siguiendo el código vemos que en la variable square_pred guardamos el valor de Ypred2 . En margin_square guardamos el valor de max(margin-Ypred, 0)2. A partir de aquí sustituyendo en la ecuación las variables nos da como resultado la expresión contenida en la línea de return.
Se puede encontrar mucha más información del porqué de los cálculos en los siguientes artículos:
https://towardsdatascience.com/contrastive-loss-explaned-159f2d4a87ec
https://medium.com/@maksym.bekuzarov/losses-explained-contrastive-loss-f8f57fe32246
Parte común del modelo.
Esta parte se va a ejecutar para las dos entradas, es la parte común del modelo y recibe una imagen como entrada, de 28 x 28.
def initialize_base_branch():
input = Input(shape=(28,28,), name="base_input")
x = Flatten(name="flatten_input")(input)
x = Dense(128, activation='relu', name="first_base_dense")(x)
x = Dropout(0.3, name="first_dropout")(x)
x = Dense(128, activation='relu', name="second_base_dense")(x)
x = Dropout(0.3, name="second_dropout")(x)
x = Dense(128, activation='relu', name="third_base_dense")(x)
#Returning a Model, with input and outputs, not just a group of layers.
return Model(inputs=input, outputs=x)
base_model = initialize_base_branch()
He creado una función para contener el código de esta parte del modelo. Es un modelo muy simple, pero puede complicarse mucho más, aquí es donde podríamos crear la estructura de capas que consideremos necesaria para aprender a tratar los datos que le vayamos a pasar.
Hay que fijarse que lo que la función devuelve es un modelo, no un grupo de capas, con su entrada y su salida.
A este modelo tendremos que sumarles las capas de entrada y la de salida de un modelo Siames.
Capas de entrada y de salida del modelo Siames.
#Input for the left part of the pair. We are going to pass training_pairs[:,0] to his layer.
input_l = Input(shape=(28, 28,), name='left_input')
#ATENTION!!! base_model is not a function, is model and we are adding our input layer.
vect_output_l = base_model(input_l)
#Input layer for the right part of the siamse model. Will receive: training_pairs[:,1]
input_r = Input(shape=(28, 28,), name='right_input')
vect_output_r = base_model(input_r)
#The lambda output layer calling the euclidenan distances, will return the difference between both vectors
output = Lambda(euclidean_distance, name='output_layer',
output_shape=eucl_dist_output_shape)([vect_output_l, vect_output_r])
#Our model have two inputs and one output. Each of the inputs contains the commom model.
model = Model([input_l, input_r], output)
Definimos dos bloques de capa de entrada + modelo común. Uno lo llamamos input_l y al otro input_r. De left y right en inglés, es decir, el bloque izquierdo y el derecho. Cada bloque recibirá una parte del conjunto de datos que hemos preparado. En la llamada al método fit del modelo veremos cómo se pasa una pareja al lado izquierdo y otro al derecho.
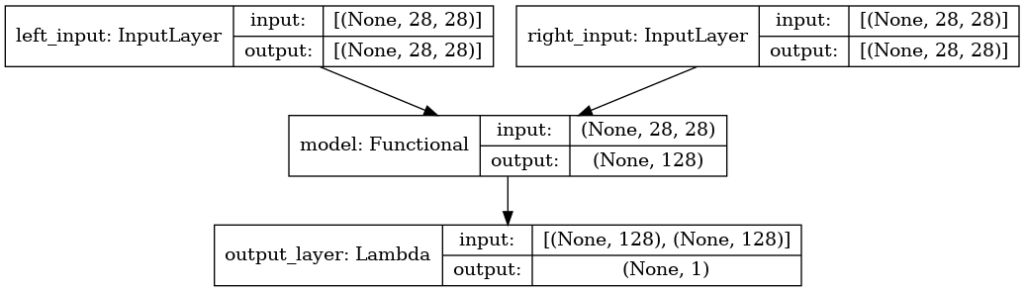
La capa de salida se crea usando una capa de tipo Lambda que llama a las dos funciones creadas antes, la que calcula la distancia euclideana, que será el retorno esperado, y la que modifica el shape de la salida.
Para crear el modelo se llama a la función Model pasandole las dos capas de entrada y la de salida.
rms = RMSprop()
#We use the 'Custom' loss function. And we can pass the margin. I'ts one of the variables
#in the formula, and mantain the balance between the value assigned when there are similarities or not.
#with a big value the dissimilarities have more weight than the similarities.
#you can try different values, I have the impression that we can increase the values and maybe improve
#a little bit the results.
#I choose to use an 1. Totally balanced.
model.compile(loss=contrastive_loss_with_margin(margin=1),
optimizer=rms)
history = model.fit(
[training_pairs[:,0], training_pairs[:,1]],
training_labels, epochs=20,
batch_size=128,
validation_data = ([val_pairs[:, 0], val_pairs[:, 1]], val_labels
Se puede ver en la llamada fit como estamos pasando los datos preparados por la función create_pairs, en la izquierda el elemento [0] y en la derecha el elemento [1]
Veamos los resultados.
16 parejas de números escogidas al azar y no hay ni un solo error. Si lo probáis en el notebook de kaggle, podréis ver qué se pueden ir realizando ejecuciones y que encontrar un error es casi imposible. Es verdad que hay número que esta muy cerca de estar mal clasificados. La pareja de seises de la segunda fila nos da un score de 0.47…. unas décimas mas y lo tomaría como un número diferente.
Pero tengamos en cuenta que hemos realizado el entreno con un solo cruce de datos! Podríamos haber cruzado cada número con dos iguales y dos diferentes, obteniendo muchos más datos para el entreno. En estos tipos de modelos las entradas son parejas de datos, por lo que cada pareja es como un dato de entrada diferente.
Conclusiones.
Me parece incredible el resultado obtenido con la red siamesa. No he trabajado demasiado con los datos, no me he preocupado del modelo, el entreno ha durado poco más de dos minutos. No he usado funciones de callback para tocar el learning rate, ni siquiera me he preocupado de gravar el mejor modelo…. y aún así el resultado es realmente muy bueno.
Las redes siamesas son muy potentes para realizar comprobaciones de parejas de datos, o para comprobar si un dato pertenece o no a un grupo. Se pueden entrenar teniendo un juego de datos limitado y ofrecen un resultado espectacular.
Claro que no va a ser así para todos los Datasets, y no siempre pueden usarse. Pero en los casos en los que sea posible, y son muchos, nos ofrecen una solución muy optima.
En casos de reconocimiento facial 1 to 1 se deben tener muy en cuenta. Debido a la poca capacidad de proceso necesario. Son ideales incluso para equipos con recursos limitados, como dispositivos IoT.
En el primer post de preparar la certificación de TensorFlow Developer, vimos el notebook preparado para solucionar un problema de Read more
Bueno, pues después de unos meses de preparación y unos días de nervios. Decidí presentarme al examen para obtener el Read more
En mi trabajo tengo relación con varios equipos de desarrollo, uno de ellos dedica una buena parte de su tiempo Read more
En el artículo anterior, aprendimos a montar un prompt que era capaz de generar órdenes SQL desde peticiones realizadas en Read more